Making a Neural Network from Scratch
August 24, 2023
In this blog post, we’ll walk through the process of building a basic neural network using Python. Neural networks are the foundation of many modern AI applications, including image recognition and natural language processing.
Understanding Neural Networks
A neural network is composed of many layers which consist of neurons, hence getting the name neural network relating to a human brain. The first layer which takes in the input is called an input layer, then comes hidden layers which may be many in number depending on the NN and the final layer is an output layer. Each hidden layer takes the input from the previous layer and passes its output to the next layer until it reaches the output layers and is shown to the user.
Each layer consists of many neurons which receive input from the user or from another node. Each input is given a weight depicted with the letter w, which is assigned on the relative importance to the other inputs. There is an additional value bias (b) which is associated with an input which is a constant that is added to the products of the input and weight. The final equation of all this looks like this:
output = sum (weights(W) * inputs(X)) + bias (b)Sigmoid Function
The sigmoid function is a special form of the logistic function and is usually denoted by σ(x) or sig(x). It is given by:
σ(x) = 1/(1+exp(-x))The sigmoid function is used as an activation function in neural networks. The sigmoid function guarantees that the output will always lie between 0 and 1. Also, as the sigmoid is a nonlinear function, the output of this unit would be a nonlinear function of the weighted sum of inputs.
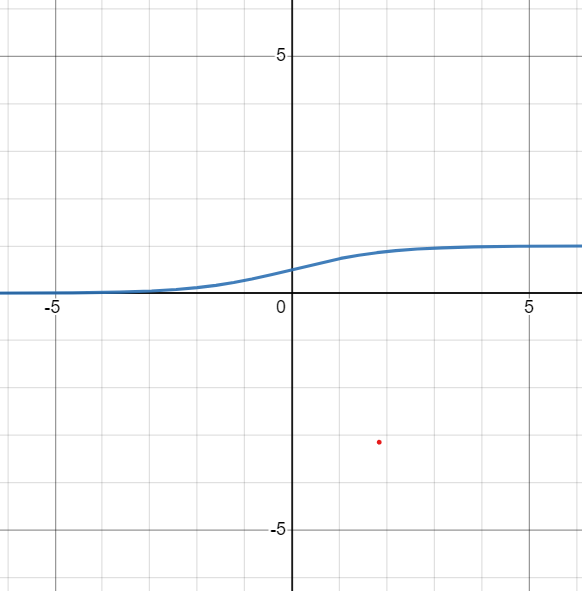
Sigmoid Functions always return the value between 0 and 1.
Backpropagation
This is an algorithm that is designed to test for errors working back from output nodes to input nodes. Backpropagation involves updating the weights and bias to minimize the error. We adjust the weights and bias based on how much they contributed to the error.
Implementing the Neural Network
Let’s implement a simple neural network using Python and the NumPy library. This network will have an input layer, a hidden layer, and an output layer.
import numpy as np
# Input data (features)
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
# Corresponding target labels
y = np.array([[0], [1], [1], [0]])
# Activation function (sigmoid)
def sigmoid(x):
return 1 / (1 + np.exp(-x))The first code snippet shows importing numpy and then setting up input variable and target variable. It then defines the sigmoid function we talked about which takes in the input and returns a value between 1 and 0.
# Initialize weights and biases
input_size = 2
hidden_size = 2
output_size = 1
learning_rate = 0.1
weights_input_hidden = np.random.uniform(size=(input_size, hidden_size))
biases_hidden = np.zeros((1, hidden_size))
weights_hidden_output = np.random.uniform(size=(hidden_size, output_size))
bias_output = np.zeros((1, output_size))Setting weights that will be modified (these are set randomly).
# Training loop
for epoch in range(10000):
# Forward pass
hidden_layer_input = np.dot(X, weights_input_hidden) + biases_hidden
hidden_layer_output = sigmoid(hidden_layer_input)
output_layer_input = np.dot(hidden_layer_output, weights_hidden_output) + bias_output
predicted_output = sigmoid(output_layer_input)
# Calculate loss
loss = np.mean(0.5 * (y - predicted_output)**2)
# Backpropagation
error = y - predicted_output
d_output = error * predicted_output * (1 - predicted_output)
error_hidden = d_output.dot(weights_hidden_output.T)
d_hidden = error_hidden * hidden_layer_output * (1 - hidden_layer_output)
# Update weights and biases
weights_hidden_output += hidden_layer_output.T.dot(d_output) * learning_rate
bias_output += np.sum(d_output, axis=0, keepdims=True) * learning_rate
weights_input_hidden += X.T.dot(d_hidden) * learning_rate
biases_hidden += np.sum(d_hidden, axis=0) * learning_rateFinally we use backpropagation to minimize the error by modifying the weights. Our error is the difference between the target and predicted variables. d_output is calculated by multiplying the error by the derivative of the sigmoid function applied to the output of the final layer. The derivative of the sigmoid function is used to compute how much the output should change to reduce the error.
print("Final predictions:", predicted_output)And that’s it you’ve made a neural network! Print the final predictions and see how well your neural network performed by crosschecking with the target labels.